Hooke’s law: definition, formulae, stress-strain curve with [PDF]

Welcome back to The Mechanical post! Today we’ll discuss What is Hooke’s law? its definition, what is elastic and plastic deformation, stress-strain diagram of ductile and brittle materials.

To download the PDF on Hooke’s law, click on the button provided at the end.

Before starting make sure you are well acquainted with the properties of a material. (The link would open up in another tab so that you can enjoy reading this article.) 

Now, let’s start off by defining stress and strain:

 Definition of stress

Stress is defined as the ratio of the force acting on the body to the area on which the force acts.

Mathematically, σ = W / A

where, σ = Stress-induced
           W = Force applied
           A = Area on which force is acting   The SI unit of stress is Newton/millimeter ² (N/mm²)  

Definition of strain

Strain is defined as the “Ratio of change in dimension of the body to the original dimension of the body when an external load is applied to it”.

Mathematically speaking,

Strain = Change in dimension / Original dimension

The strain is a unitless quantity.

Before we learn about Hooke’s law of elasticity, let us know the terms, “plastic and elastic deformation”.

Deformation means a change in shape and size.

What is Elastic deformation?

Elastic deformation is a type of deformation wherein the body comes back to its original shape and size when the deforming force is removed.

Let’s understand it with an example of a spring. It is fixed at one end and on the other end, some weight is applied. This results in the stretching of the spring or says it gets deformed. At the same time, an internal restoring force of the same magnitude is induced in it. This force resists the deformation of the spring.

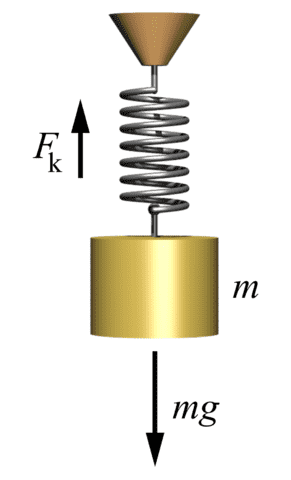
In equilibrium conditions, the magnitude of external force and the internal resistive force would be the same but in different directions. Now, when the weight i.e. the external force is removed, the magnitude of the external force becomes 0, however, the internal force remains the same. This internal force causes the spring to come back to its original shape and size.

This is known as elastic deformation. It must be noted that elastic deformation is possible to a certain extent of loading, beyond that the body enters the plastic deformation zone.

What is meant by Plastic deformation?

Taking the same example of spring as above, but now we increase the weight to a greater extent. What would happen if we kept increasing the load? This would result in more elongation of the spring. At one point, the external force would become far greater than the internal resistive force. This would result in the permanent deformation of the spring. In simple words, the spring would not be able to regain its original shape and size.

So we can now, define plastic deformation as:

Plastic deformation is the type of deformation in which the applied load when removed, results in a permanent set or permanent deformation of the body. 

 In plastic deformation, the body doesn’t regain its original shape and size. All materials undergo elastic as well as plastic deformation. A material remains until the elastic limit, beyond that plastic deformation occurs. Every material has its own elastic limit.  

The stress-strain curve helps in understanding whether the material would get elastically or plastically deformed under particular loading circumstances.

What is Hooke’s law?

In 1660, Robert Hooke an English scientist stated an empirical law which today is widely known as the Hooke’s law. Empirical means based on observations and experiences. So let’s see what is Hooke’s law.

Hooke’s law states that ” For an elastic deformation in the body, the deforming force is directly proportional to the change in length”.   

Let us understand it with the example of the spring,   Suppose a force (F) acts upon the spring in the downward direction, causing an increase in the length of the spring, say (x) as shown in the figure below.

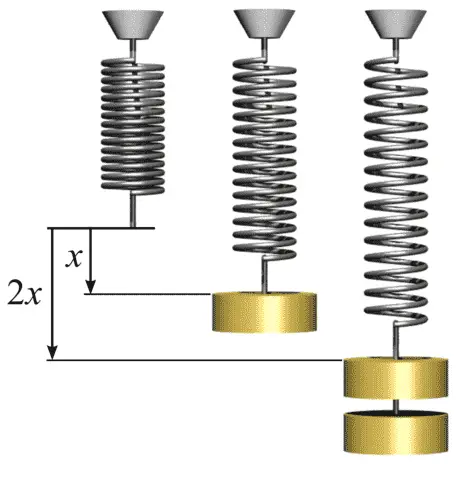
 Then according to Hooke’s law of elasticity, the deforming force (F) is directly proportional to change in length (x).   

i.e F α x i.e F = k.x   – where k is constant of proportionality   

Similarly, if the force is increased to 2F, the change in length gets increased by 2x.

It is also written as F = – k.x   

Why the negative sign? allow me to explain it to you.  

We can also define Hooke’s law in a slightly different manner, i.e. The restoring force is directly proportional to the change in length. Here instead of deforming force, restoring force is considered.

Due to this, the magnitude remains the same, however, the direction of the restoring force is in the opposite direction of change in length, hence the – ve sign. There’s another modified version of Hooke’s law which states:  

The stress induced in a material is directly proportional to the strain within its elastic limit.

  i.e. Stress α Strain (only under the elastic limit)  

Stress-strain diagram for ductile material

The below figure shows the stress-strain diagram of mild steel (ductile material). Ductile materials like aluminum, copper, steel, etc follow the same pattern.   A specimen made up of mild steel with uniform cross-section is taken and put under tensile test in a Universal testing machine UTM. The specimen is loaded until it breaks. When plotted as a graph we get the following results. (see fig below).  

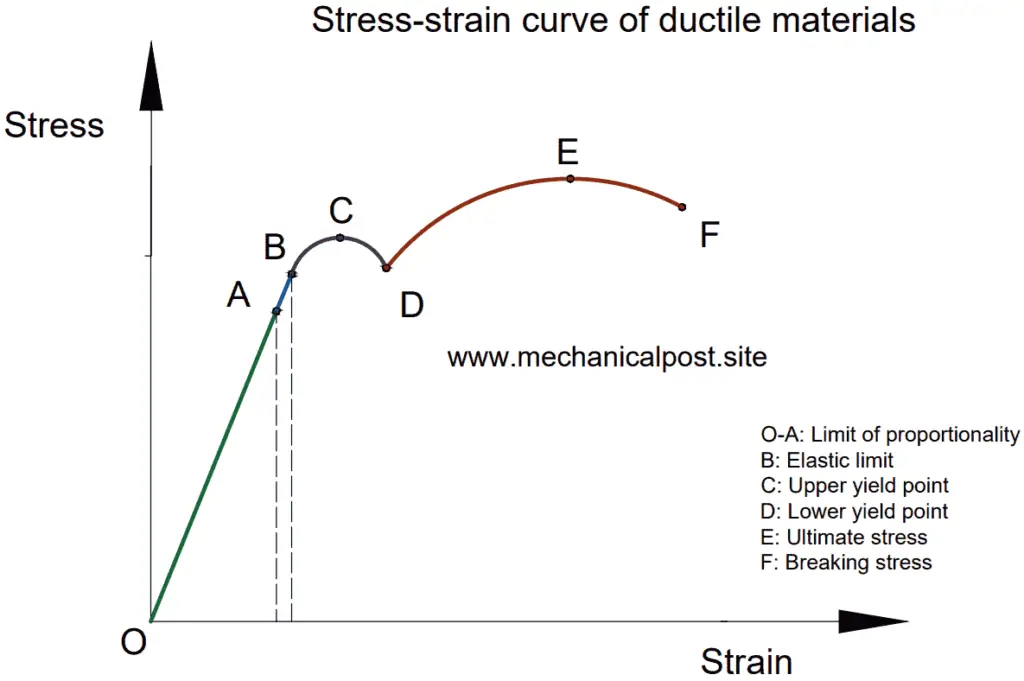
Explanation of stress strain curve of ductile material:

Point O-A: The straight line of O-A represents that the stress is directly proportional to strain. Point A is known as the “limit of proportionality”. In this phase as the stress increases, the strain also increases in the same proportion.   

Point B: This point is known as the “Elastic limit”. The material is elastic when loaded under point B. So, during this period if the load is removed, the material will come back to its original shape and size. However, if the material is loaded beyond point B the material will not regain its shape and size. From here onwards, plastic deformation starts. Beyond this point, Hooke’s law is not obeyed.

Point C: Point C is known as the “Upper yield point”. As the load is increased beyond point B, the strain in the material increases rapidly with a very small increase in stress, hence the curve formation.

Point D: Point D is called the “lower yield point”. When we go beyond point C, the strain increases at a high rate. This condition is known as plastic flow. A very small amount of stress is needed to maintain the deformation of the material.  

Point E: Point E is known as the “Ultimate stress”. At point E, the stress is at the highest, hence the name, ultimate stress. After point D, we can see a sudden rise in stress and strain. During this period the cross-sectional area of the specimen decreases considerably.  

Point F: Point F is “Breaking stress”. Between points, E and F the cross-sectional area of the specimen reduce such that neck formation can be seen. At this point, the stress needed to break the specimen is very low, even less than the ultimate stress, hence a drop in the curve from E-F is observed.   

At the breaking stress, the specimen is broken into two. Thus this point is known as the breaking point and the stress corresponding to it is known as the breaking stress.

Stress-strain diagram for brittle material

The figure below shows the stress-strain diagram of a brittle material, say for eg. cast iron. Some examples of brittle material are ceramics, cast iron, high carbon steel, etc.

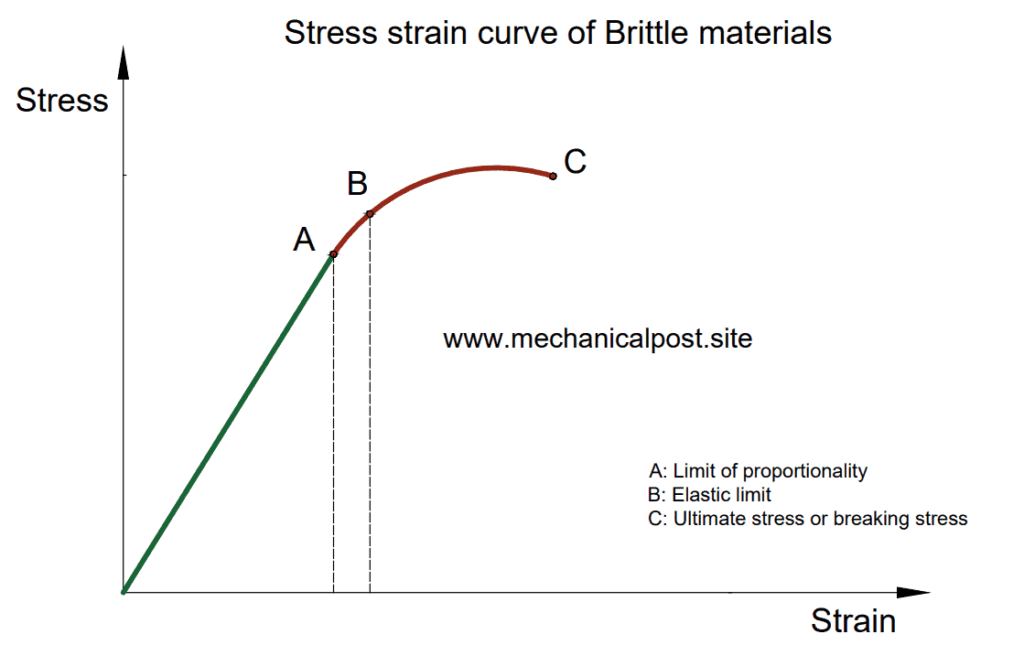
The above material shows the stress-strain relationship of a brittle material when subjected to tensile load on the UTM (universal testing machine)

Explanation of stress strain curve of brittle material:

Point O-A: Just like the ductile material, the O-A region is the one in which stress is directly proportional to strain and obeys Hooke’s law. Thus, we see a straight line. Point A is the limit of proportionality.  

Point B: It is the limit of elasticity of the material beyond this the material will be in the region of the plastic set.   

Point C: Point C is the breaking point or ultimate stress point in the brittle material. After the elastic limit, there is a sudden increase in the strain with comparatively little increase in the stress resulting in the curve. The material breaks or fails at this point. There is very little amount of plastic deformation in brittle materials when compared to ductile materials. Brittle materials fail at relatively low strain.  

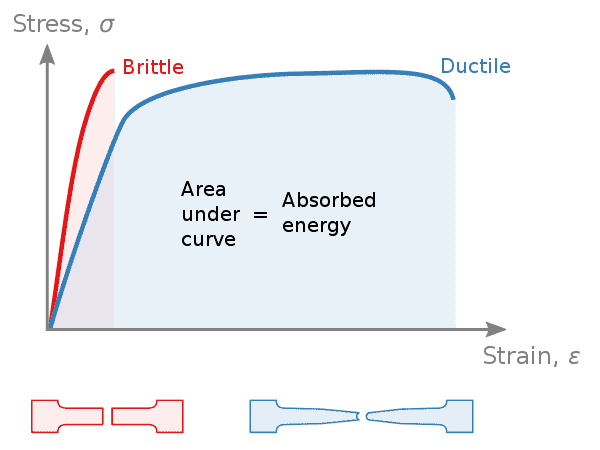
Difference between stress-strain diagram of ductile and brittle materials

The following are the differences between the graphs of ductile and brittle material

• The ductile materials generally have higher elastic limits as compared to brittle materials.
• Ductile materials go through a long process before failing. However, for brittle materials the process is short.
• This indicates that there is an ample amount of plastic deformation in ductile materials which serves as a warning that the material is failing.
• But in case of brittle materials, as there is not much plastic deformation, by the time the cracks and other changes are visible, the material fails.

• As shown in the figure above, the ductile material absorbs more energy before failing, whereas the brittle material fails abruptly.

So that’s all on Hooke’s law and stress-strain diagram. Love reading The Mechanical post? let us know the comments. Also, we are available on Telegram @TheMechanicalpost  do check us out there!

The Mechanical post will be back! till then keep reading and learning.